گاز ایده‌آل (ناصر همامی 890180371 مهندسی نفت شیمی عمومی)مطلب ارسالی ازnasser homami

گاز ایده‌آل یک تقریب از گازهای حقیقی است که برای مقاصد محاسباتی بکار می‌رود. گاز ایده‌آل به گازی گفته می‌شود که:

بین ذرات آن نیرویی وجود نداشته باشد و تنها برهم‌کنش بین ذرات، برخورد صلب باشد.
اندازهٔ ذرات نسبت به مسیر آزاد میانگین ناچیز باشد.

گازهای حقیقی را در چگالی‌های پایین با تقریب خوبی می‌توان ایده‌آل فرض کرد.

گازهای ایده‌آل در حالت تعادل داخلی از معادلهٔ گاز ایده‌آل پیروی می‌کنند:

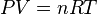
$PV=nRT$

که در آن P فشار داخلی سیستم، V حجم سیستم، n تعداد مول‌های ذرات سیستم، R ثابت جهانی گازها و T دمای سیستم با یکای کلوین است.

رای اثبات این قانون، اول لازم است که با قانون‌های بویل و شارل آشنا شویم .

قانون بویل

رابطهٔ بین فشار و حجم یک گاز در 1662 میلادی توسط رابرت بویل ( Robert Boyle ) اندازه گیری شد . بویل متوجه شد که افزایش فشار وارد شده بر یک گاز با کاهش حجم آن متناسب است . اگر فشار دو برابر شود، حجم به نصف کاهش می‌یابد . اگر فشار سه برابر شود، حجم به یک سوم حجم اولیه اش می‌رسد . قانون بویل می‌گوید که در دمای ثابت، حجم گاز با فشار رابطهٔ عکس دارد :

$V \propto \frac{1}{P}$

قانون شارل

رابطهٔ بین حجم و دمای یک گاز در 1787 میلادی توسط ژاک شارل ( Jacques Charles ) مطالعه شد و نتایج او به طور قابل ملاحظه‌ای توسط شاگردانش ژوزف گیلوساک ( Joseph Gay - Lussac ) گسترش یافت . براساس این قانون حجم تمام گازها، در فشار ثابت، با دمای مطلق آن گاز رابطهٔ مستقیم دارد :

$V \propto T$

قانون گازهای ایده آل

در دما و فشار ثابت حجم یک گاز با تعداد مول‌های آن نسبت مستقیم دارد . حجم یک مول گاز نصف حجم اشغال شده توسط 2 مول گاز می‌باشد . بنابراین قانون و قوانین بویل و شارل می‌توان گفت که :

$V \propto (\frac{1}{P})(T)(n)$

با استفاده از یک عدد ثابت می‌توان تناسب را به تساوی تبدیل کرد :

$V=R(\frac{1}{P})(T)(n)$

که از آن نتیجه می‌شود :

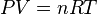
$PV=nRT$

قانون گازهای ایده آل توسط نظریهٔ جنبشی گازها

نمونه‌ای از یک گاز شامل N (عدد آووگادرو) مولکول، هر کدام با جرم m را در نظر بگیرید. اگر این نمونه در مکعبی با یال a باشد، حجم آن برابر خواهد شد با:

$V=a^3$

با فرض اینکه یک سوم مولکول‌ها در جهت محور x، و دو سوم در جهت محورهای y و z حرکت کنند، آنگاه در هر ۲a حرکت یک مولکول گاز در جهت محور x داخل مکعب، مولکول حداقل یکبار به دیوارهٔ مکعب برخورد می‌کند. با فرض اینکه سرعت میانگین هر مولکول گاز برابر u است، در هر ثانیه هر مولکول گاز به اندازهٔ $\frac {u}{2a}$ برخورد دارد و در هر برخورد به اندازهٔ ۲mu اندازهٔ حرکت آن تغییر می‌کند. پس در هر ثانیه هر مولکول گاز به اندازهٔ زیر به دیوارهٔ مکعب نیرو وارد می‌کند :

$(\frac {u}{2a})(2mu)= \frac {mu^2}{a}$

از این رو برای تمام مولکولهای گاز می‌توان نوشت :

$(\frac{N}{3}) (\frac{mu^2}{a})$

فشار عبارت است از نیرو بر سطح. پس :

$P = \frac{\tfrac {Nmu^2}{3a}}{a^2} = \frac {Nmu^2}{3a^3} = \frac {Nmu^2}{3V}$

پس می‌توان نوشت :

$PV = \frac {1}{3} Nmu^2 = (\tfrac {2}{3} N) (\tfrac {1}{2} mu^2) = \tfrac {2}{3} N (KE)$

که KE در آن میانگین انرژی جنبشی مولکولی گاز می‌باشد. و از آنجا که انرزی جنبشی یک گاز (بنابر نظریه جنبشی گازها) با دمای مطلق آن نسبت مستقیم دارد و همچنین $N \propto n$ ، پس :

$N (KE) \propto nT$

که با ضرب کردن عدد ثابتی مثل R، می‌توان تناسب را به تساوی تبدیل کرد :

$PV=nRT$

تاریخ: 2 ارديبهشت 1391برچسب:گاز ایده‌آل,

ارسال توسط

گازهای ایده آلمطلب ارسالی ازشاهین پارسایی نیا

گاز ایده‌آل

ایزوترم‌های یک گاز ایده آل

1. بین ذرات آن نیرویی وجود نداشته باشد و تنها برهم‌کنش بین ذرات، برخورد صلب باشد.

2. اندازهٔ ذرات نسبت به مسیر آزاد میانگین ناچیز باشد.

گازهای حقیقی را در چگالی‌های پایین با تقریب خوبی می‌توان ایده‌آل فرض کرد.

قانون گازهای ایده‌آل

گازهای ایده‌آل در حالت تعادل داخلی از معادلهٔ گاز ایده‌آل پیروی می‌کنند:

که در آن P فشار داخلی سیستم، V حجم سیستم، n تعداد مول‌های ذرات سیستم، Rثابت جهانی گازها و T دمای سیستم با یکای کلوین است.

اثبات

برای اثبات این قانون، اول لازم است که با قانون‌های بویل و شارل آشنا شویم .

قانون بویل

قانون شارل

قانون گازهای ایده آل

با استفاده از یک عدد ثابت می‌توان تناسب را به تساوی تبدیل کرد :

که از آن نتیجه می‌شود :

قانون گازهای ایده آل توسط نظریهٔ جنبشی گازها

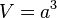
با فرض اینکه یک سوم مولکول‌ها در جهت محور x، و دو سوم در جهت محورهای y و z حرکت کنند، آنگاه در هر ۲a حرکت یک مولکول گاز در جهت محور x داخل مکعب، مولکول حداقل یکبار به دیوارهٔ مکعب برخورد می‌کند. با فرض اینکه سرعت میانگین هر مولکول گاز برابر u است، در هر ثانیه هر مولکول گاز به اندازهٔ برخورد دارد و در هر برخورد به اندازهٔ ۲muاندازهٔ حرکت آن تغییر می‌کند. پس در هر ثانیه هر مولکول گاز به اندازهٔ زیر به دیوارهٔ مکعب نیرو وارد می‌کند :

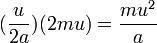
از این رو برای تمام مولکولهای گاز می‌توان نوشت :

فشار عبارت است از نیرو بر سطح. پس :

پس می‌توان نوشت :

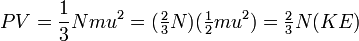
که KE در آن میانگین انرژی جنبشی مولکولی گاز می‌باشد. و از آنجا که انرزی جنبشی یک گاز (بنابر نظریه جنبشی گازها) با دمای مطلق آن نسبت مستقیم دارد و همچنین ، پس :

که با ضرب کردن عدد ثابتی مثل R، می‌توان تناسب را به تساوی تبدیل کرد :

جستارهای وابسته

بنویت پال امیل کلاپيرون

منابع

شیمی عمومی ( جلد اول )، چارلز مورتیمر، دکتر عیسی یاوری، نشر علوم دانشگاهی، تهران ، 1385 ، ISBN 964-6186-30-0

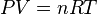
فیزیک ( جلد دوم )، رابرت رزنیک، دیوید هالیدی، کنت اس . کرین، دکتر جلال الدین پاشایی راد، دکتر محمد خرمی، محمد رضا بهاری، مرکز نشر دانشگاهی، تهران ، 1381 ،

تاریخ: 2 فروردين 1391برچسب:گاز ایده‌آل,قانون گازهای ایده‌آل,

ارسال توسط

آخرین مطالب

تعداد گزارش کارهای دریافت شده به همراه نام فرستنده

نمرات شیمی عمومی 2 زیست شناسی

نمرات شمی الی گروه زیست شناسی

حلالیت sA:کربوکسیلیک ایذهای تک عاملی با 5 اتم کربن یا کمترمطلب ارسالی ازصبا ادیب پرور

مطلب ارسالی ازfaezehaboomahboob

فواید و خواص دارویی اجزای درخت سرومطلب ارسالی ازصبا ادیب پرور

خواص کاجمطلب ارسالی ازصبا ادیب پرور

استخراجمطلب ارسالی ازشیدا محمدی

استخراجمطلب ارسالی ازصبا ادیب پرور

آزمایش تابعیت حلالیت از درجه حرارتمطلب ارسالی ازمهدی قره باغی

صفحه قبل 1 2 3 4 5 ... 22 صفحه بعد


	نام :
	وب :
	پیام :
	2+2=:


(Refresh)

قانون بویل

قانون گازهای ایده آل

قانون گازهای ایده آل توسط نظریهٔ جنبشی گازها

قالب وبلاگ